题目描述
给定两个整型数组$A,B$,长度分别为$n,m$,且均为单调不下降序列。给定整数$k$,求出第$k$小值。
输入格式
第一行三个整数,分别表示$n,m,k$;
第二行$n$个整数,表示数组$A_i$;
第二行$m$个整数,表示数组$B_i$.
输出格式
一个整数表示第$k$小值.
样例
1
2
3
| 4 6 8
1 3 6 7
0 2 4 5 9 11
|
提示
$1 \leq n,m \leq 10^7,1 \leq k \leq m+n, 0 \leq A_i,B_i<2^{64}-1$
Sol.1 双指针扫描
时间复杂度$O(n)$
不赘述
Sol.2 中位数BFPRT
时间复杂度$O(\log n)$
BFPRT 求有序数组中位数
可以通过递归求解计算,时间复杂度$O(\log n)$
比如,我们有如下长度为$10$(偶数)的两个有序数组$a,b$:
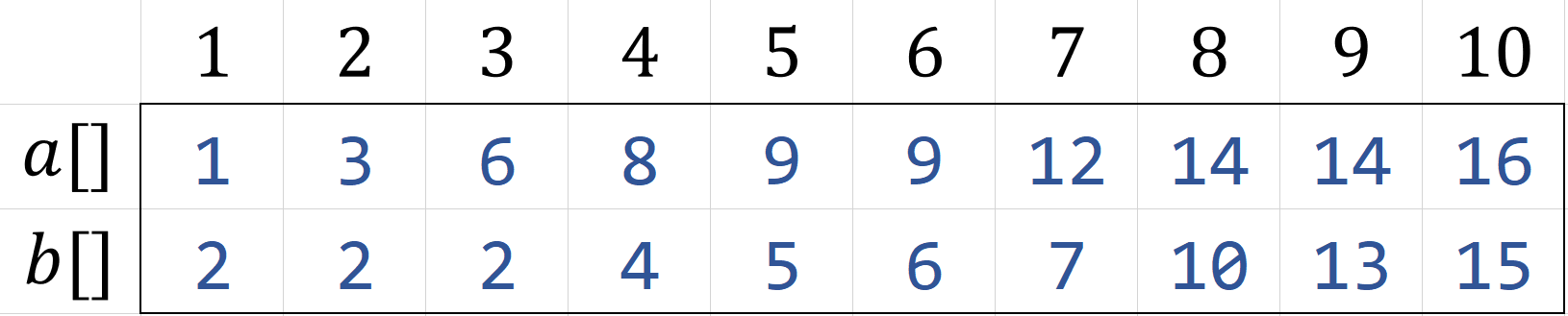
我们取每个数组中位数进行比较
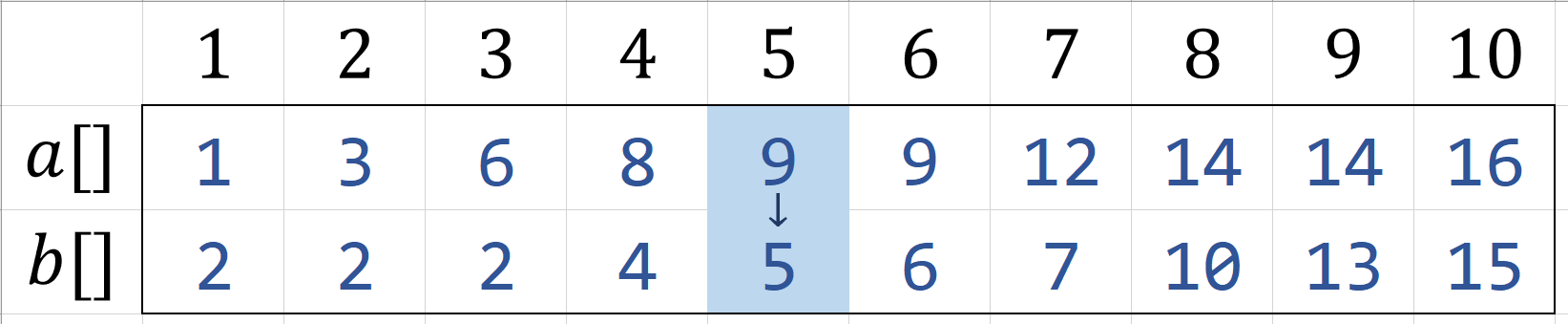
若$A[mid]>B[mid]$,那么,显然中位数不会出现在标黄色区域
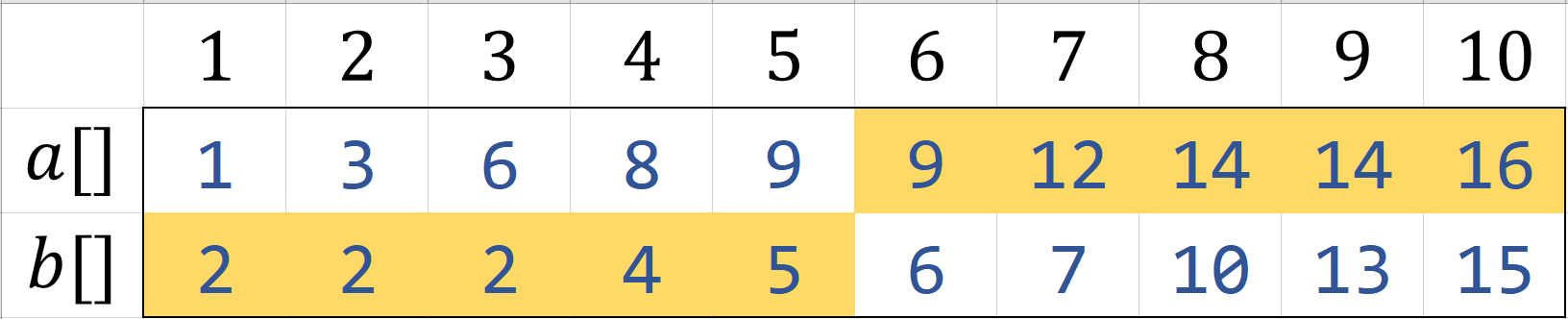
那么我们只需要在蓝色区间内查找中位数
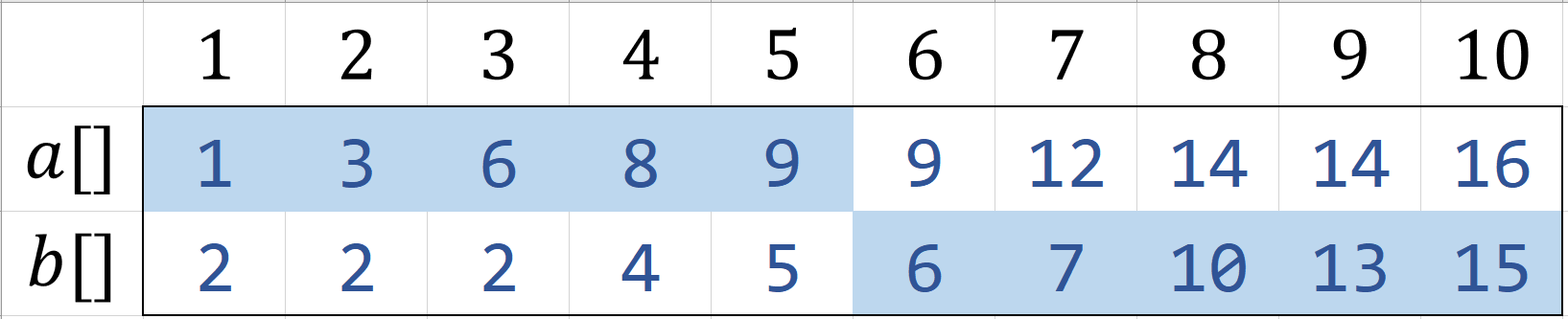
此时我们有如下长度为$5$(奇数)的两个有序数组$a,b$:
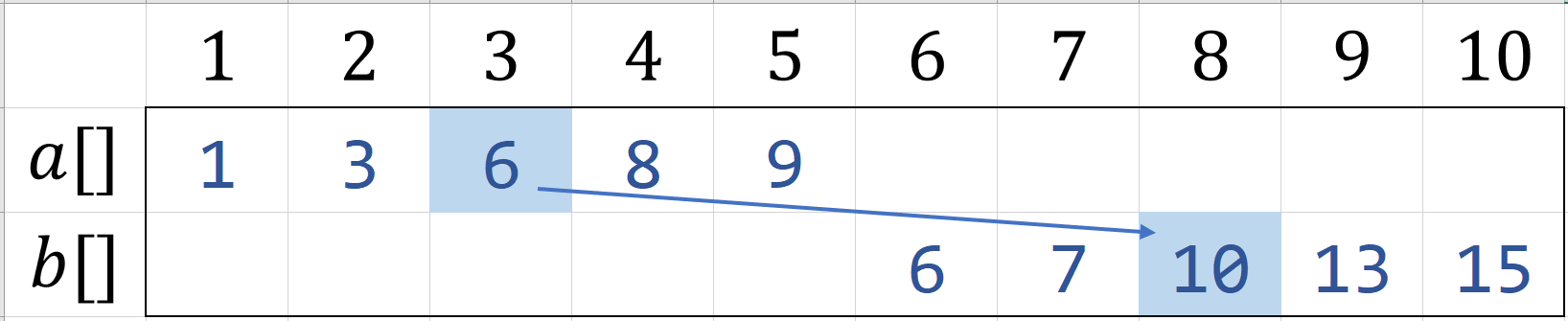
若$A[mid]<B[mid]$,那么,显然中位数不会出现在标黄色区域
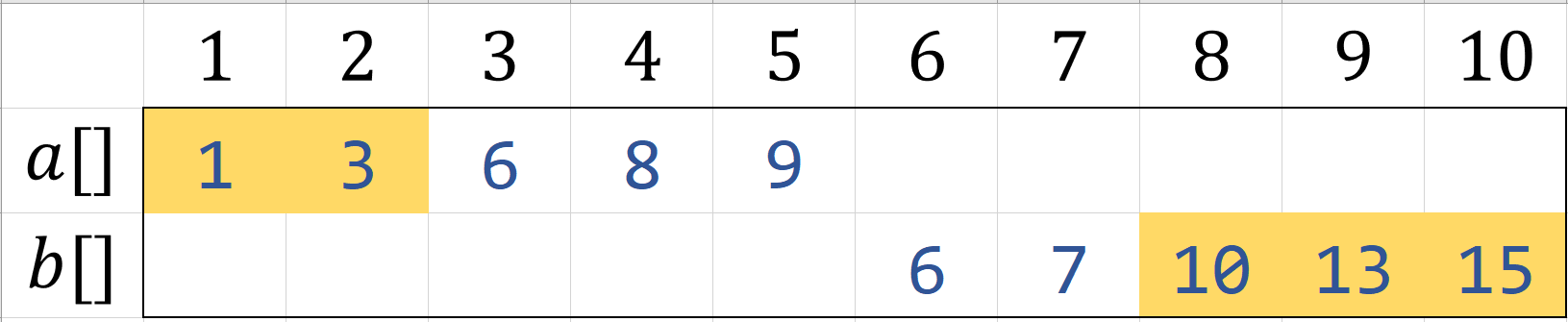
但是当我们去掉不可能的部分后,剩下的部分长度不等
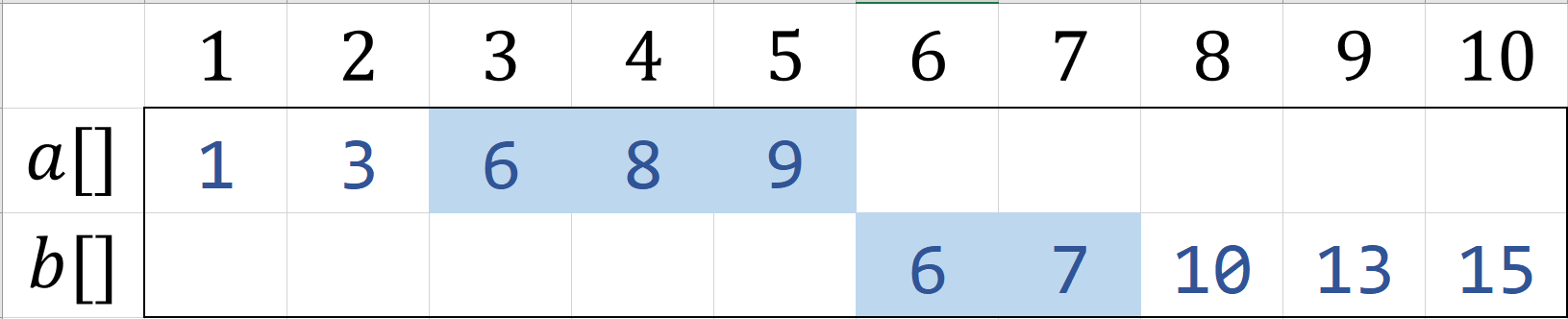
此时我们可以把$A[mid]$与$B[mid-1]$比较
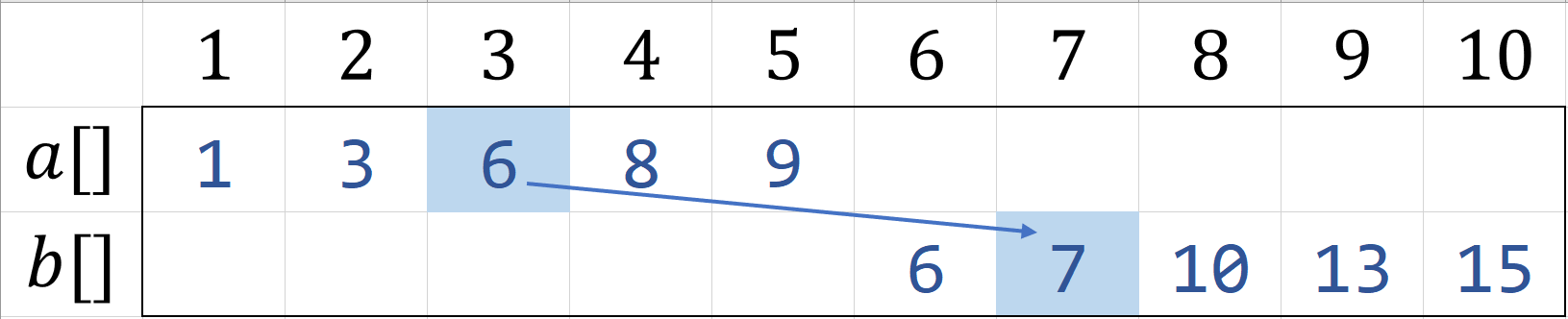
若$A[mid] \geq B[mid-1]$那么可以断定$A[mid]$就是中位数
若$A[mid] < B[mid-1]$ ,那么继续递归转到下一次寻找中位数
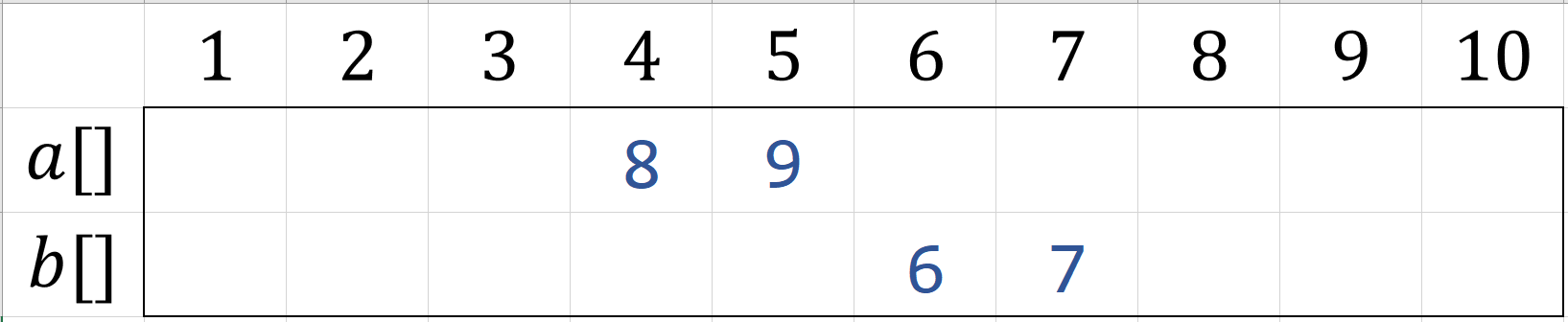
直到最后每个数组只剩$1$个数,返回其中较小值即可
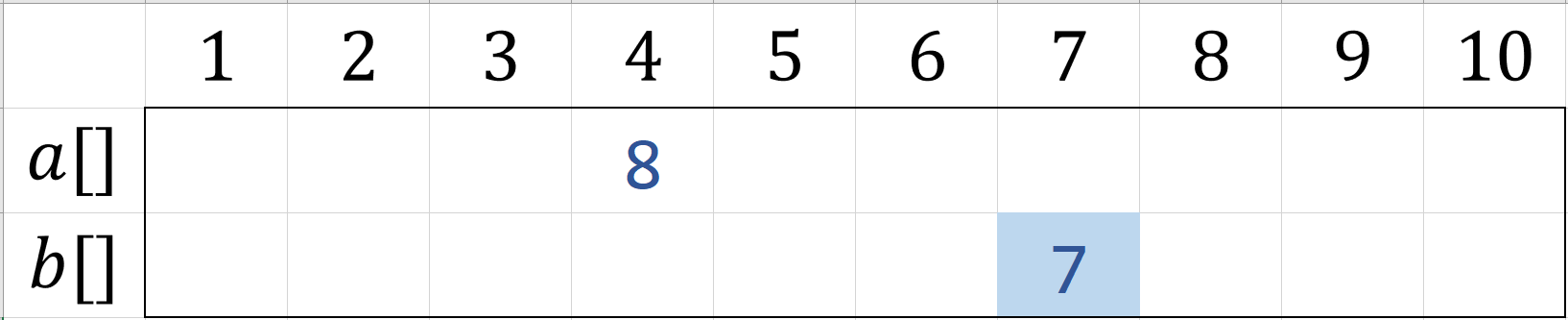
在本例中,中位数为$7$.
若上述某一步奇偶性或大小表示不同,那么相反操作即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| int dfs(int sa,int ea,int sb,int eb){
if(sa==ea)return min(a[sa],b[sb]);
int ma=(sa+ea)>>1,mb=(sb+eb)>>1;
bool ji=(ea-sa+1)&1;
if(a[ma]>b[mb]){
if(ji){
if(b[mb]>=a[ma-1]) return b[mb];
else return dfs(sa,ma-1,mb+1,eb);
}else return dfs(sa,ma,mb+1,eb);
}else{
if(ji){
if(a[ma]>=b[mb-1]) return a[ma];
else return dfs(ma+1,ea,sb,mb-1);
}else return dfs(ma+1,ea,sb,mb);
}
}
|
利用BFPRT求第K小值
如给定如下有序数组$a,b$
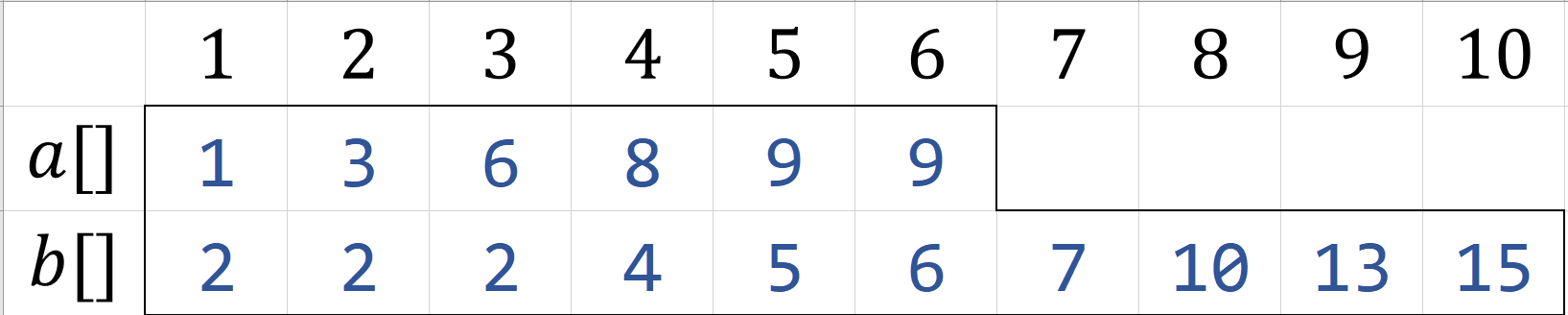
长度分别为$n=6,m=10$
对于给定的$K$,分三种讨论
- $K \leq \min(n,m)$
- $\min(n,m) \leq K \leq \max(n,m)$
- $\max(n,m) \leq K$
对于第一种,若$K=4$,我们只需要对$a[1 \to K],b[1 \to K]$进行求中位数即可
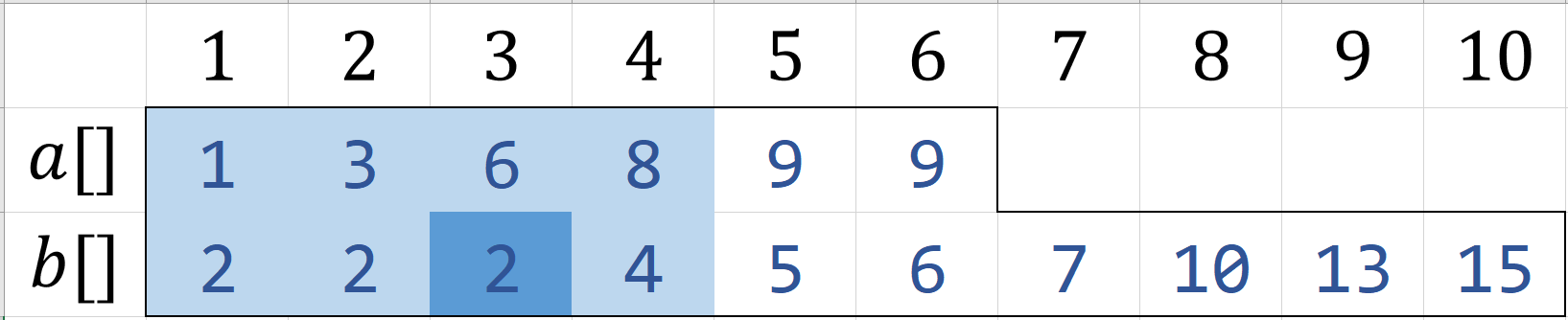
即$2$
1
2
3
| int solve1(){
return dfs(1,k,1,k);
}
|
对于第二种,若$K=8$
因为在本例中$n<m$,我们需要对$b[K-n]$特判(若$n>m$则交换$a,b$)
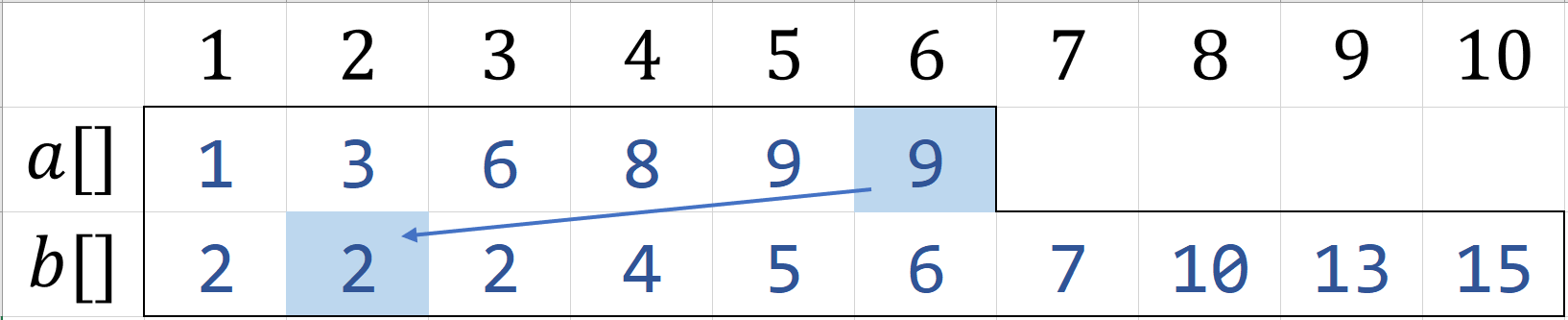
若$b[K-n] \geq a[n]$,那么$b[K-n]$就是第$K$小值
若$b[K-n] < a[n]$,那么对$a[1 \to n],b[K-n+1 \to K]$进行求中位数即可

即$6$
1
2
3
4
5
6
7
8
9
| int solve2(){
if(n<m){
if(b[k-n]>=a[n]) return b[k-n];
else return dfs(1,n,k+1-n,k);
}else{
if(a[k-m]>=b[m]) return a[k-m];
else return dfs(k+1-m,k,1,m);
}
}
|
对于第三种,若$K=12$
我们需要对$b[K-n],a[K-m]$特判
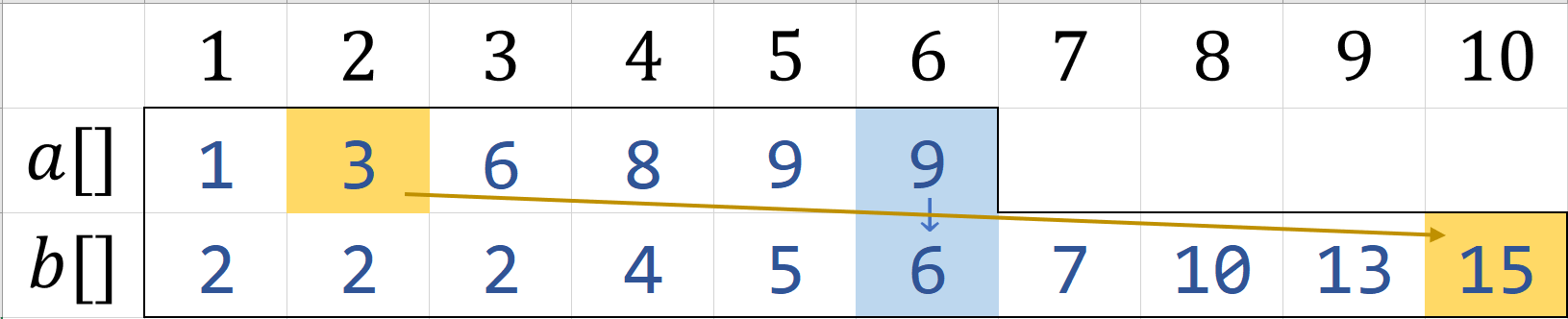
若$b[K-n] \geq a[n]$,那么$b[K-n]$就是第$K$小值
若$a[K-m] \geq b[n]$,那么$a[K-m]$就是第$K$小值
若$b[K-n] < a[n] \And a[K-m] < b[n]$,那么对$a[K-m+1 \to n],b[K-n+1 \to m]$进行求中位数即可
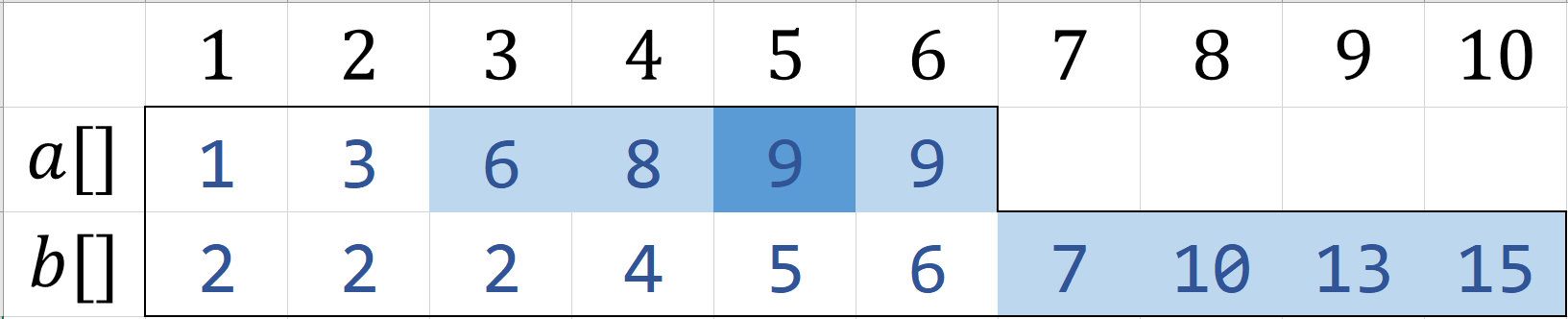
即$9$
1
2
3
4
5
| int solve3(){
if(a[k-m]>=b[m]) return a[k-m];
else if(b[k-n]>=a[n]) return b[k-n];
else return dfs(k+1-m,n,k+1-n,m);
}
|
总体时间复杂度全部在BFPRT求中位数上,复杂度为$O(\log n)$
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| #include<iostream>
#define min(x,y) ((x)>(y)?(y):(x))
#define max(x,y) ((x)<(y)?(y):(x))
using namespace std;
inline long long read(){
long long x=0,f=1;char c=getchar();
for(;!isdigit(c);c=getchar())if(c=='-')f=-1;
for(;isdigit(c);c=getchar())x=(x<<3)+(x<<1)+(c^48);
return x*f;
}
long long n,m,k,a[10000005],b[10000005];
long long dfs(long long sa,long long ea,long long sb,long long eb){
if(sa==ea)return min(a[sa],b[sb]);
long long ma=(sa+ea)>>1,mb=(sb+eb)>>1;
bool ji=(ea-sa+1)&1;
if(a[ma]>b[mb]){
if(ji){
if(b[mb]>=a[ma-1]){
return b[mb];
}else{
return dfs(sa,ma-1,mb+1,eb);
}
}else{
return dfs(sa,ma,mb+1,eb);
}
}else{
if(ji){
if(a[ma]>=b[mb-1]){
return a[ma];
}else{
return dfs(ma+1,ea,sb,mb-1);
}
}else{
return dfs(ma+1,ea,sb,mb);
}
}
}
void solve1(){
cout<<dfs(1,k,1,k);
}
void solve2(){
if(n<m){
if(b[k-n]>=a[n]) cout<<b[k-n];
else cout<<dfs(1,n,k+1-n,k);
}else{
if(a[k-m]>=b[m]) cout<<a[k-m];
else cout<<dfs(k+1-m,k,1,m);
}
}
void solve3(){
if(a[k-m]>=b[m]) cout<<a[k-m];
else if(b[k-n]>=a[n]) cout<<b[k-n];
else cout<<dfs(k+1-m,n,k+1-n,m);
}
int main(){
n=read(),m=read(),k=read();
for(long long i = 1;i<=n;i++) a[i]=read();
for(long long i = 1;i<=m;i++) b[i]=read();
long long minn=min(n,m),maxn=max(n,m);
if(k<=minn) solve1();
else if(k>minn && k<=maxn) solve2();
else solve3();
}
|















